I’ve been modeling the dynamic issuance policy we are using right now for 1hive in order to assess it’s suitability for Gardens, and I’ve found pretty interesting things.
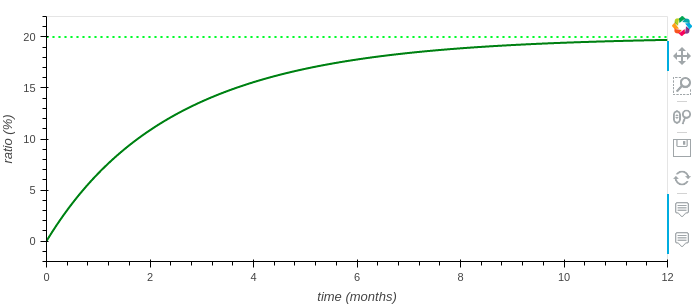
First of all, this is how it looks like when we have an inflationary policy (it can fulfill the common pool up to 20% in one year):
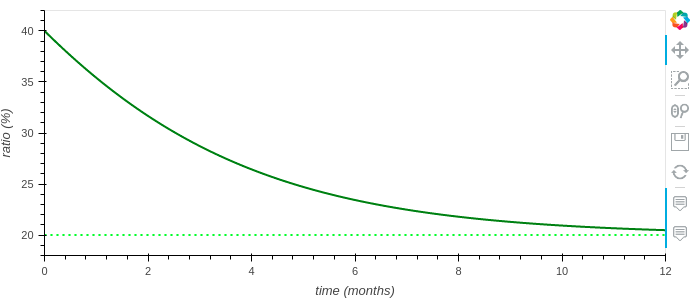
And this is when we enter in deflationary policy (current ratio is higher than target ratio):
If we apply a throttle to the previous charts (max adjustment parameter), we can see how the curve is flat during the first months because we don’t want a very high inflation during any point in time:
And the same happens in deflation if we apply a low enough throttle:
You can play with this model in this jupyter notebook I’ve created (click on Runtime > Run all to play with the sliders).
Some considerations
After playing with the model, I’ve found some problems that I would like to see solved in subsequent versions of the issuance policy, and especially in the one which we will start future gardens.
The current policy doesn’t follow a predictable formula
The current implementation of the formula is iterative. This means that the token supply is adjusted every time a function of the smart contract is called.
This makes difficult to calculate the supply of the token in for example one year from now. The method we can use is to loop 365 times on the adjustment function to find the final common pool balance and token supply. Ideally it should have a formula f(x) where x is the time from now so we can calculate the ratio between the common pool and the token supply.
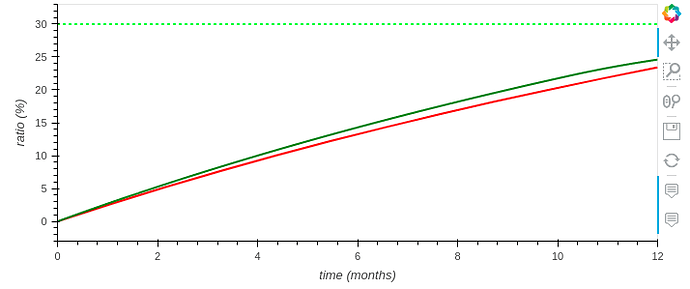
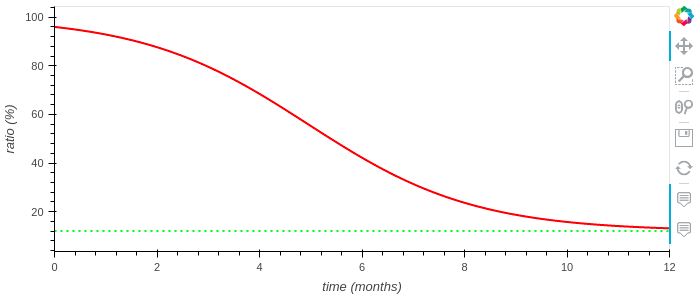
Another problem it has is that due to this iterative behavior, the issuance changes depending on when the function in the smart contract is called. It doesn’t change significantly when it’s called every day, but the divergence is easily observable if we call it once a month (red line):
Parameter name “max adjustment per year” may be misleading
A “max adjustment per year” of 10% doesn’t mean that in one year the total supply won’t increase or decrease more than 10%. For example, setting the initial ratio to 0% and the target ratio is 30% with a “max adjustment per year” of 10%, we see how the total supply is increased by +32.5% in just one year.
We say that it is “max adjustment per year” because the smart contract is requiring a “max adjustment per second” parameter, and we use an annualized input instead. I think it might be misleading so I would simply use the word “throttle” to name this parameter.
The policy acts differently when the ratios are high
Because of the nature of the formula used to calculate the adjustments, it have some odd behaviors when the current or target ratio are high.
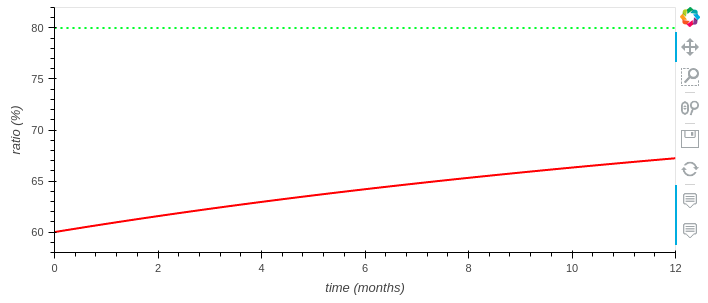
When the target ratio is 80% it takes much more to fill the funding pool than when it is 20% (compare with the first chart):
When the current ratio is very high (most of the tokens are in the funding pool), it burns the tokens in a quite strange way:
If you think this is inconsistent, and we could have a nicer issuance policy, I’ve a proposal:
Let’s hack on a better issuance policy!
This is an open call for the Luna Swarm  to discuss about the issues with the current dynamic issuance policy and propose a new formula that fits better. Maybe these issues are not concerning enough to change HNY issuance policy, but a Dynamic Issuance v2 with these things solved would be nice before we start the Gardens economies.
to discuss about the issues with the current dynamic issuance policy and propose a new formula that fits better. Maybe these issues are not concerning enough to change HNY issuance policy, but a Dynamic Issuance v2 with these things solved would be nice before we start the Gardens economies.